Speeding Up Geodesic Tracing in geometry-central

As part of some recent work in procedural mesh generation, I’ve been working with a computational geometry library called geometry-central to trace geodesic paths on the surface of 3D meshes. geometry-central is written in C++, and I compiled the library to WebAssembly with Emscripten in order to use it in the browser.

As I recently learned, a geodesic path is the straightest path along a surface. It’s the path you would take if you were to walk in a straight line across the surface of some manifold for some distance in some direction.

I’m using them to wrap a 2D mesh onto the surface of a 3D mesh, kind of like inverse UV mapping or a sort of variation of the “shrink wrap” modifier from Blender. After extruding the output from that, the result looks pretty cool:

I need trace up to millions of geodesic paths to generate this, and I want to do so as quickly as possible in order to make it possible to generate it dynamically. However, the initial performance numbers I was seeing weren’t very optimism-inspiring:

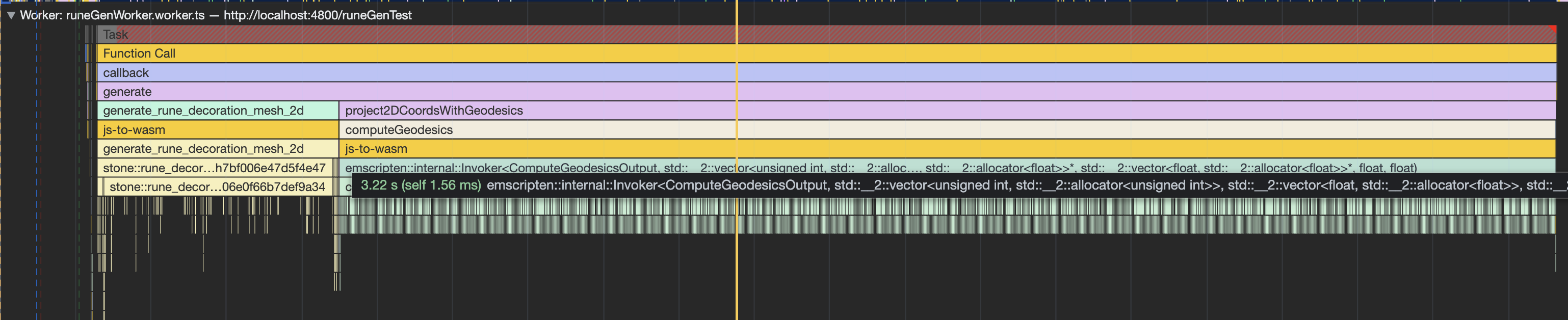
Drilling in further, it became clear that some functions from the Eigen linear algebra library named ColPivHouseholder were the bottleneck of the process:

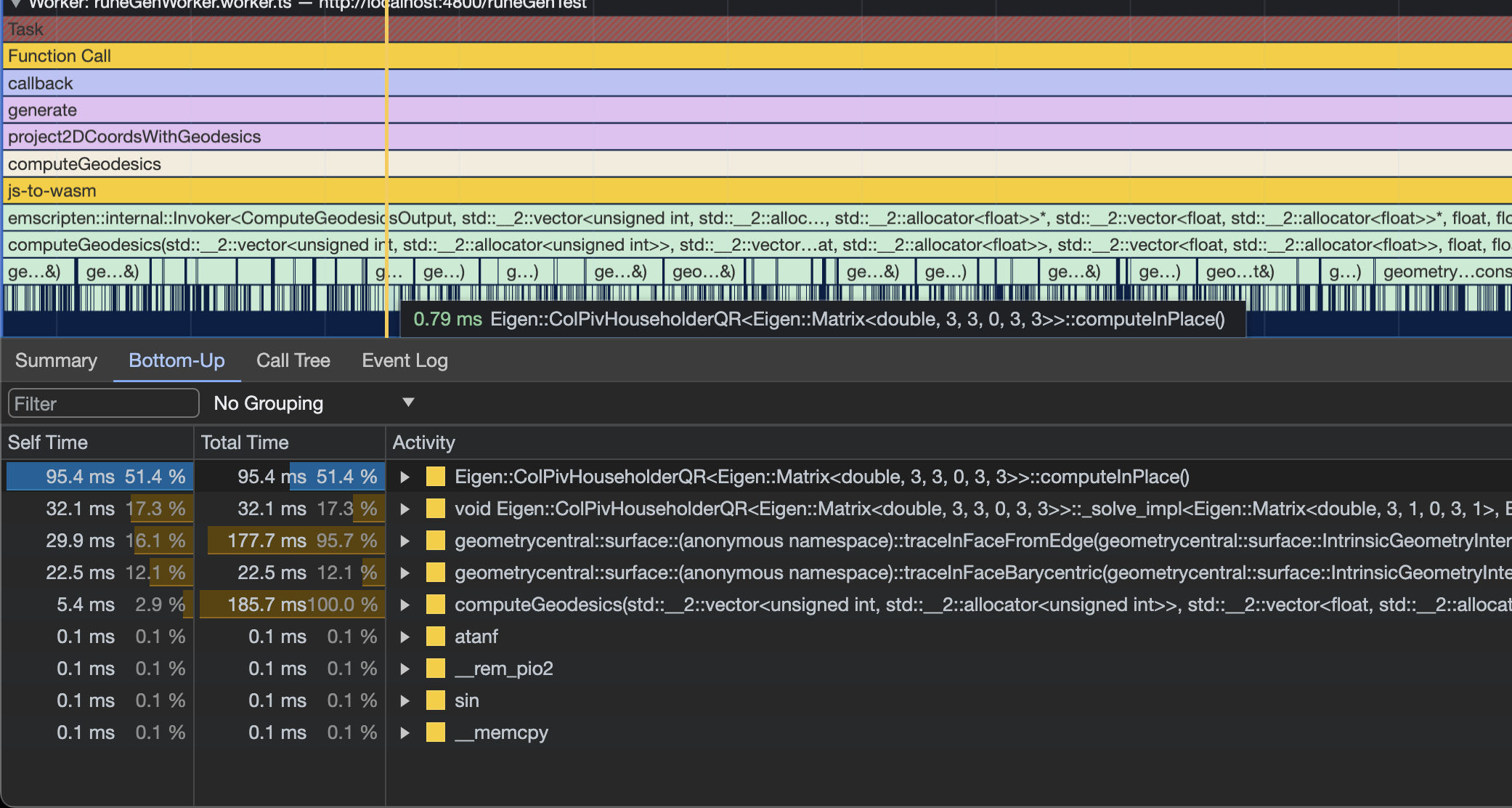
I found the function in the geometry-central code where this was getting called. It was part of the logic for converting cartesian coordinate to barycentric coordinates. Barycentric coordinates are a way of representing some point within a triangle as a normalized mixture of each of the triangle’s points. It is used by the geodesic path tracing process.

Here’s the code itself:

inline Vector3 normalizeBarycentricDisplacement(Vector3 baryVec) {
  double s = sum(baryVec);
  return baryVec - Vector3::constant(s / 3.);
}

inline Vector3 cartesianVectorToBarycentric(const std::array<Vector2, 3>& vertCoords, Vector2 faceVec) {
  // Build matrix for linear transform problem
  // (last constraint comes from chosing the displacement vector with sum = 0)
  Eigen::Matrix3d A;
  Eigen::Vector3d rhs;
  const std::array<Vector2, 3>& c = vertCoords; // short name
  A << c[0].x, c[1].x, c[2].x, c[0].y, c[1].y, c[2].y, 1., 1., 1.;
  rhs << faceVec.x, faceVec.y, 0.;

  // Solve
  Eigen::Vector3d result = A.colPivHouseholderQr().solve(rhs);
  Vector3 resultBary{result(0), result(1), result(2)};

  resultBary = normalizeBarycentricDisplacement(resultBary);

  return resultBary;
}

geometry-central chose to implement the conversion by solving the system of equations directly via one of Eigen’s built-in solvers. This is a totally valid and correct way to handle it, but as you might imagine it leaves a lot of performance on the table.

The data has to be copied into the Eigen matrices, the solver has to do whatever initialization and cleanup it needs to, and then there’s that additional normalizeBarycentricDisplacement operation at the end that I don’t quite understand the purpose of.

Since we know we’re doing Cartesian -> barycentric coordinate conversion, we can use a bit of a more specific algorithm than what Eigen might be doing here.

I found some code on Gamedev Stack Exchange that itself was based on code from http://realtimecollisiondetection.net/ by Christer Ericson that implements the conversion process using simple math operations inline. I made some small tweaks to get the coordinates looking exactly like they did using Eigen, and wound up with this equivalent code:

inline Vector3 cartesianVectorToBarycentric(const std::array<Vector2, 3>& vertCoords, Vector2 faceVec) {
  Vector2 v0 = vertCoords[1] - vertCoords[0];
  Vector2 v1 = vertCoords[2] - vertCoords[0];
  Vector2 v2 = faceVec - vertCoords[0];

  double d00 = dot(v0, v0);
  double d01 = dot(v0, v1);
  double d11 = dot(v1, v1);
  double d20 = dot(v2, v0);
  double d21 = dot(v2, v1);
  double denom = d00 * d11 - d01 * d01;

  double v = (d11 * d20 - d01 * d21) / denom;
  double w = (d00 * d21 - d01 * d20) / denom;
  double u = 0. - v - w;
  return Vector3{u, v, w};
}

Results⌗

Well is it faster? Yep!

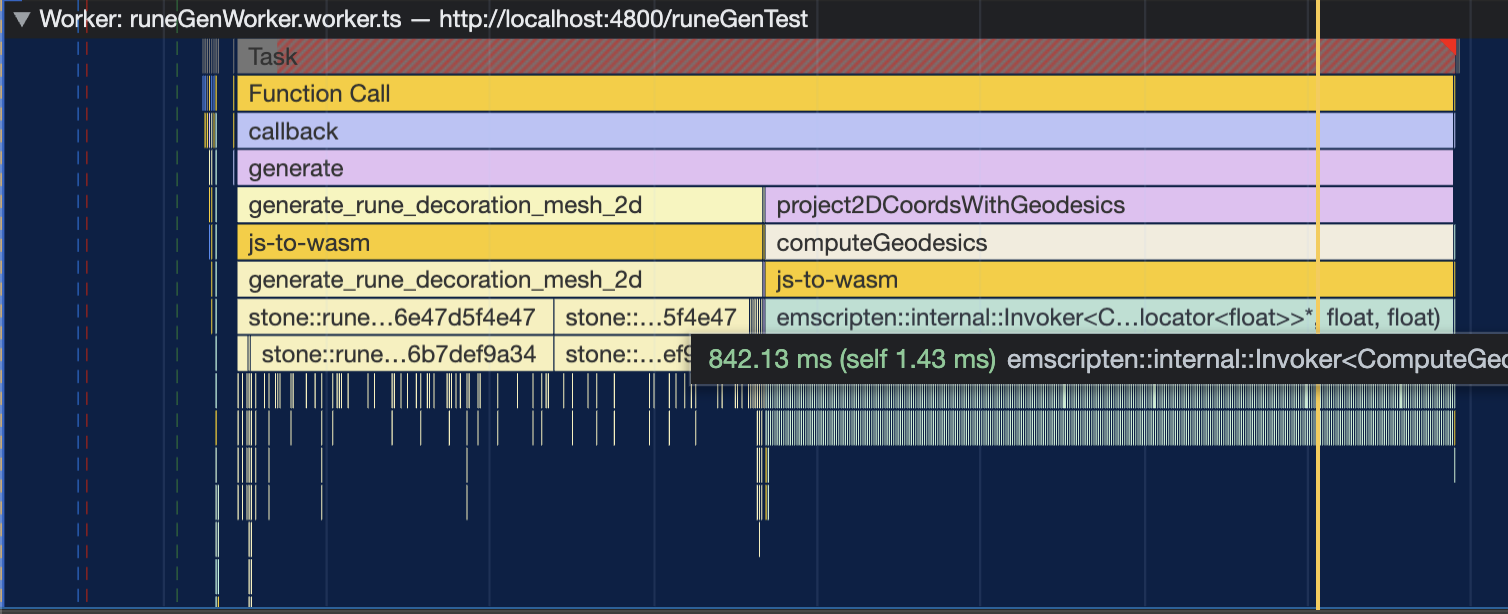
The entire function is over 3x faster and there’s other stuff going on besides this barycentric coordinate conversion, so the speedup for that is even greater. This should now be fast enough for my purposes.

If I need more, the answer on stack exchange points out that a lot of the computations in that function can be pre-computed per triangle since they don’t depend on the input Cartesian coordinates. I’m not sure how much of an impact that would actually make for this case, though, but it’s an option to pursue if needed.

It was very nice to find an easy to spot bottleneck and a pre-made optimization I was able to drop in with little effort.

I pushed up these changes to a fork of geometry-central if you’re interested in using them directly.