I recently finished some work involving constrained bezier curves for use in my browser-based digital audio workstation. Specifically, I used them in its envelope generator, which looks like this:

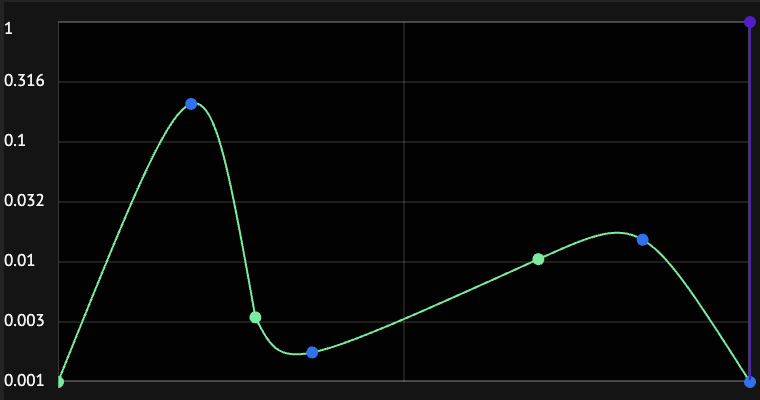
A screenshot of the envelope generator for web synth showing the bezier curves used to define the curves that are joined together to produce the transfer function.

The circles are draggable handles that allow the user to create whatever shape they desire for the envelope. The green handles define the start and end point of each curve segment and the blue circles control its shape/steepness.

Motivation⌗

Originally, I used the function x^n to build the curves that made up the envelope. This curve type worked decently well and allowed for curves of varying steepness to be represented, but it had some problems:

  • The x^n function can produce numerically unstable results with very large or very small exponents. This can result in very rapid changes in underlying value or even produce NaN or Infinity values. As you might imagine, isn’t very good for audio use cases.
  • Curves aren’t symmetrical going in vs. going out which makes it impossible to create symmetrical peaks/dips, which is something often desired.

So the main goal was to add support for a different curve type that would solve these problems and ideally add options for even more expressive shapes than before.

Bezier curves were an obvious choice due to how simple they are to implement and their wide adoption. However, they also pose some challenges of their own:

  • If x^n didn’t offer enough control over the shape of the curve, Bezier curves offer too much control. For example, it’s possible to create bezier curves that loop back in the X dimension like this:

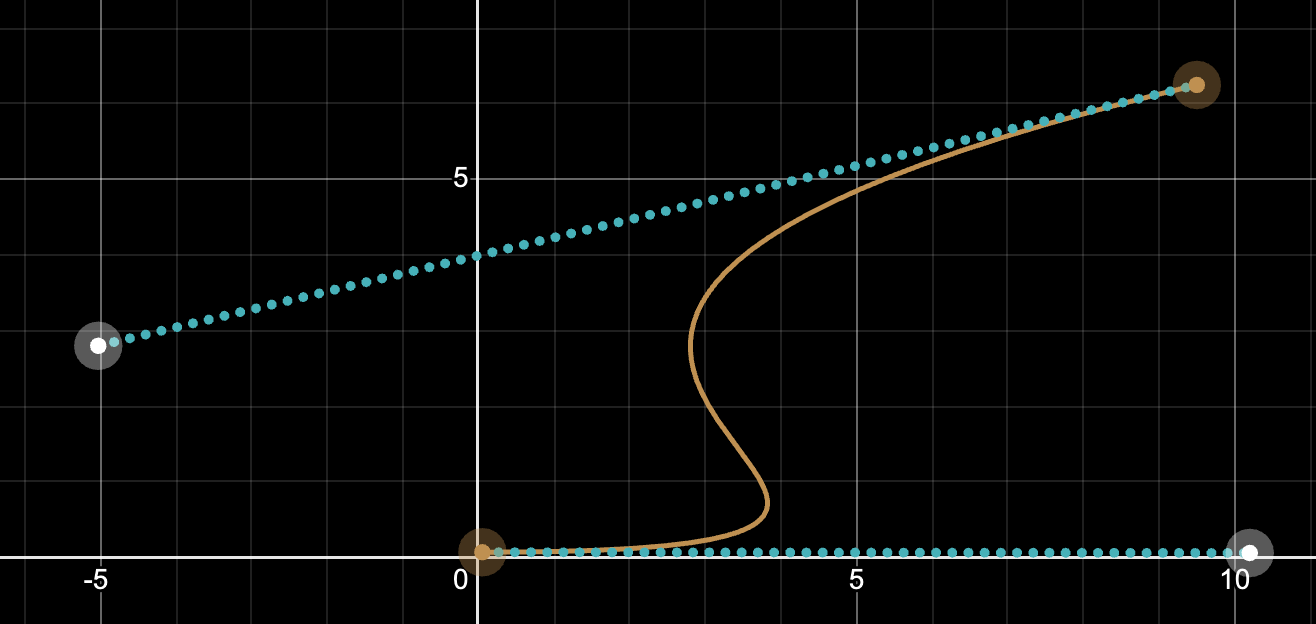
A screenshot of a bezier curve with a X coordinate that increases, decreases, and then increases again along its span - making a sort of “s” shape.

This clearly makes no sense for an envelope generator use case. I needed a way to constrain the generated curves in a way that ensures they’re valid.

  • The control points - which are used to adjust the shape of the curve - don’t lie on the curve itself. To work nicely in my existing UI, I needed to be able to add a handle somewhere on the curve that could be dragged to adjust its shape directly.
  • Additionally, for cubic bezier splines, there are two different control points which need to be selected to shape the curve. I needed a way to pick values for these behind the scenes from a single handle position.

Constrained Bezier Curves⌗

A cubic bezier curve is defined by four points: A start point (P0), end point (P3), and two control points (P1 and P2). The start and end point of the curves are fixed, so all we have to worry about is picking values for the two control points.

I experimented with some bezier curve editors and manually tested out some different control point patterns. I eventually realized that setting both control points to the same position worked quite well and get me very close to what I was looking for.

It turns out that this produces curves with a lot of desirable characteristics. Crucially, the curves’ X values all monotonically increase/decrease along the span of the curve, so no looping back or other degenerate curve shapes can be created.

One important property of bezier curves which I learned is that all points on the curve will fit within the convex hull of the points that define it. So, if the control points are set to a position within the rectangle bounded by the start and end points, all resulting curves should be valid.

Although a lot of possible curve shapes aren’t creatable with coincident control points, it still provides more than enough control over the shape of the curve. So, I decided to stick with this method to constrain the curves.

Computing Control Points⌗

The final piece to figure out was a way to control the shape of the curve by dragging a handle on the curve itself rather than moving a floating control point directly.

I needed to pick a point on the curve on which to attach the handle. I experimented with a few options and quickly discovered that the midpoint of the curve by length was the obvious best choice.

Bezier curves can be defined as a linear combination of lower-degree bezier curves. At the midpoint of the curve (t=0.5), the direction of the curve is evenly balanced between heading towards the shared control point and heading towards the endpoint. This works out to producing an instantaneous direction that is parallel to the line from the start point to the endpoint.

Anyway, now remainder of problem is quite well defined. P0 and P3 are already defined and fixed. There’s a constraint that the resulting curve must pass through the handle’s position (H) at t=0.5. Given that, we have to solve for the shared control point (C).

Here is the formula for a constrained cubic Bezier curve using coincident control points:

$$ConstrainedBezier(t) = (1 - t)^3 P_0 + 3 (1 - t)^2 t C + 3 (1 - t)t^2 C + t^3 P_3$$

This can be simplified using some algebra into the following:

$$ConstrainedBezier(t) = (1 - t)^3 P_0 + 3t(1 - t)C + t^3P_3$$

Then, to solve for the position of the handle H, we can plug its t=0.5 value into the equation:

$$H = ConstrainedBezier(t) = (1 - 0.5)^3 P_0 + 3 \times 0.5 (1 - 0.5)C + 0.5^3P_3$$

Those constants collapse down, and after re-arranging H and C and applying a bit more algebra, we get the following equation yielding the position of the shared control point:

$$C = \frac{1}{6} P_0 + \frac{4}{3} H + \frac{1}{6} P_3$$

I was pretty surprised that the solution ended up being so simple - a linear combination of the start point, end point, and handle position. Sure enough, when I plugged them in, I reliably got out control points that generated curves which accurately intersected the handles at the curves’ midpoints.

Here’s how it looks all put together:

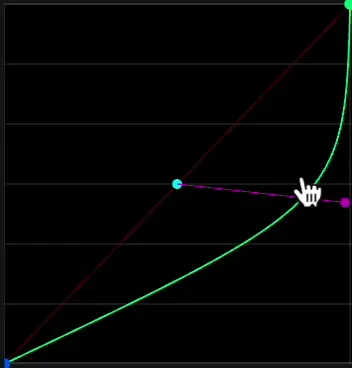
A screen recording of the envelope generator using the constrained Bezier curve with some additional debug elements showing the position of the computed control point in pink, a line between the start and end point in dark red, and a line from the control point to the midpoint between the start and end point in pink. The draggable handle also always sits on that line no matter where the handle is dragged.

Dragging the handle adjusts the curve in a way that feels intuitive and responsive. I was very happy with how it ended up feeling to use this.

The pink circle is the computed shared control point for the curve. As a final step, I clamp that control point to be within the bounds of the envelope segment and then re-calculate the handle position using that clamped value. This ensures that the curve always remains valid and produces values that are in bounds.

One other thing I noticed while setting this up is that the control point and handle always end up on the same line as the midpoint between the start and end point (this is drawn in pink in the animation above).

Conclusion⌗

That’s about it! I just wrote this up because I thought the properties of cubic bezier curves with coincident control points ended up being very neat and potentially useful in other domains.

I’m very happy with how this ended up working in the envelope generator itself as well. The curves look beautiful and seem to be working very well for generating musically interesting envelopes.